Interpoler une fonction de répartition des salaires à partir de quantiles connus

[ MAJ du 28/06/2023 : le modèle présenté dans cet article a été étoffé ici.]

Introduction

Cet article est assez technique et est destiné à documenter le calcul de la position d’un salaire dans la distribution des salaires du secteur privé dans notre Observatoire des salaires des enseignants.
Si vous êtes intéressé par les animations de convergence et la précision obtenue, rendez-vous directement dans la dernière partie de l’article, mais si vous avez quelques bases en analyse numérique et êtes intéressé par le type d’interpolation utilisé, vous pourrez trouver dans ce qui suit quelques indications sur la méthode que nous avons utilisée.

Afin d’estimer la distribution des salaires, l’INSEE fournit un certain nombre de quantiles, qui sont en général les premier et dernier déciles, les quartiles, la médiane, ainsi que les 95ème et 99ème centiles.
L’objectif est ici de déterminer une approximation de la fonction de répartition des salaires basée sur les quantiles fournis.

Cette approximation sera réalisée en utilisant :

des arcs de fonctions cubiques pour la partie centrale située entre les quantiles fournis ;
un arc d’exponentielle de fonction quadratique pour les valeurs inférieures au plus petit quantile connu (ceci permet une croissance plus forte qu’une simple exponentielle) ;
un arc d’exponentielle de fonction affine pour les valeurs supérieures au plus grand quantile connu.

La forte croissance de la fonction de répartition des salaires pour les petits quantiles est probablement due à l’existence d’un salaire minimum empêchant aux salaires d’avoir une valeur arbitrairement petite. Étant donné qu’il s’agit d’un trait spécifique au cas étudié ici, les fonctions à utiliser dans d’autres cas de figure dépendront donc des caractéristiques de la fonction de répartition à approximer.

Fonction utilisée pour approximer la fonction de répartition

Supposons connus $n$ quantiles d’un échantillon statistique.
Notons $(x_0; y_0)$ , $(x_1; y_1)$ , $\dots$ $(x_{n-1}; y_{n-1})$ les $n$ points correspondants par lesquels doit passer la fonction de répartition (les ordonnées sont comprises entre 0 et 1 et les abscisses, tout comme les ordonnées, sont classées par ordre croissant).

On cherche une fonction $f$ de classe $\mathcal{C}^2(\mathbb{R})$ passant par ces points, et paramétrée par le vecteur $a = (a_0 \dots a_{4n})^\top$ contenant $4n+1$ coefficients, de la forme :

$f(x;a)=\left\{\begin{array}{ll}\exp(a_0x^2+a_1x+a_2) & \text{si } x \leq x_0 \\a_3x^3+a_4x^2+a_5x+a_6 & \text{si } x_0 < x \leq x_1 \\a_7x^3+a_8x^2+a_9x+a_{10}& \text{si } x_1 < x \leq x_2 \\\vdots & \vdots \\a_{4k-1}x^3+a_{4k}x^2+a_{4k+1}x+a_{4k+2} & \text{si } x_{k-1} < x \leq x_k \\\vdots & \vdots \\a_{4n-5}x^3+a_{4n-4}x^2+a_{4n-3}x+a_{4n-2} & \text{si } x_{n-2} < x \leq x_{n-1} \\1-\exp(a_{4n-1}x+a_{4n}) & \text{si } x_{n-1} < x \\\end{array}\right. .$

La fonction $f$ étant de classe $\mathcal{C}^2(\mathbb{R})$ , sa fonction de densité $f'$ est de classe $\mathcal{C}^1(\mathbb{R})$ .

Un raccordement $\mathcal{C}^2$ en chacun des $n$ points permet d’obtenir $4n$ équations ( $2n$ pour les raccordements $\mathcal{C}^0$ à droite et à gauche de chaque point, $n$ pour le raccordement $\mathcal{C}^1$ , et $n$ pour le raccordement $\mathcal{C}^2$ ).
Afin d’obtenir un système carré, on ajoute une équation de raccordement $\mathcal{C}^3$ sur le point $(x_0, y_0)$ ce qui nous donne un total de $4n+1$ équations, égal au nombre de paramètres à déterminer.

Système d’équations à résoudre

Le système à résoudre est alors le suivant :

$\left\{\begin{array}{l}\begin{array}{lclcl}\text{raccordements } \mathcal{C}^0 \text{ : } & & \\\exp(a_0x_0^2+a_1x_0+a_2) & - & y_0 & = & 0 \\a_3x_0^3+a_4x_0^2+a_5x_0+a_6 & - & y_0 & = & 0 \\a_3x_1^3+a_4x_1^2+a_5x_1+a_6 & - & y_1 & = & 0 \\a_7x_1^3+a_8x_1^2+a_9x_1+a_{10} & - & y_1 & = & 0 \\& \vdots & & \vdots & \\a_{4k-5}x_{k-1}^3+a_{4k-4}x_{k-1}^2+a_{4k-3}x_{k-1}+a_{4k-2} & - & y_{k-1} & = & 0 \\a_{4k-1}x_{k-1}^3+a_{4k}x_{k-1}^2+a_{4k+1}x_{k-1}+a_{4k+2} & - & y_{k-1} & = & 0 \\a_{4k-1}x_{k}^3+a_{4k}x_{k}^2+a_{4k+1}x_{k}+a_{4k+2} & - & y_{k} & = & 0 \\a_{4k+3}x_{k}^3+a_{4k+4}x_{k}^2+a_{4k+5}x_{k}+a_{4k+6} & - & y_{k} & = & 0 \\& \vdots & & \vdots & \\a_{4n-5}x_{n-1}^3+a_{4n-4}x_{n-1}^2+a_{4n-3}x_{n-1}+a_{4n-2} & - & y_{n-1} & = & 0 \\1-\exp(a_{4n-1}x_{n-1}+a_{4n}) & - & y_{n-1} & = & 0 \\\end{array}\\\\\begin{array}{lclcl}\text{raccordements } \mathcal{C}^1 \text{ : } & & \\(2a_0x_0+a_1)\exp(a_0x_0^2+a_1x_0+a_2) & - & (3a_3x_0^2+2a_4x_0+a_5) & = & 0 \\3a_3x_1^2+2a_4x_1+a_5 & - & (3a_7x_1^2+2a_8x_1+a_9) & = & 0 \\& \vdots & & \vdots & \\3a_{4k-5}x_{k-1}^2+2a_{4k-4}x_{k-1}+a_{4k-3} & - & (3a_{4k-1}x_{k-1}^2+2a_{4k}x_{k-1}+a_{4k+1}) & = & 0 \\3a_{4k-1}x_{k}^2+2a_{4k}x_{k}+a_{4k+1} & - & (3a_{4k+3}x_{k}^2+2a_{4k+4}x_{k}+a_{4k+5}) & = & 0 \\& \vdots & & \vdots & \\3a_{4n-5}x_{n-1}^2+2a_{4n-4}x_{n-1}+a_{4n-3} & + & a_{4n-1}\exp(a_{4n-1}x_{n-1}+a_{4n}) & = & 0 \\\end{array}\\\\\begin{array}{lclcl}\text{raccordements } \mathcal{C}^2 \text{ : } & & \\((2a_0x_0+a_1)^2+2a_0)\exp(a_0x_0^2+a_1x_0+a_2) & - & (6a_3x_0+2a_4) & = & 0 \\6a_3x_1+2a_4 & - & (6a_7x_1+2a_8) & = & 0 \\& \vdots & & \vdots & \\6a_{4k-5}x_{k-1}+2a_{4k-4} & - & (6a_{4k-1}x_{k-1}+2a_{4k}) & = & 0 \\6a_{4k-1}x_{k}+2a_{4k} & - & (6a_{4k+3}x_{k}+2a_{4k+4}) & = & 0 \\& \vdots & & \vdots & \\6a_{4n-5}x_{n-1}+2a_{4n-4} & + & a_{4n-1}^2\exp(a_{4n-1}x_{n-1}+a_{4n}) & = & 0 \\\end{array}\\\\\begin{array}{lcl}\text{raccordement } \mathcal{C}^3 \text{ : } & & \\(8a_0^3x_0^3+6a_0(2a_0x_0+a_1)(a_1x_0+1)+a_1^3)\exp(a_0x_0^2+a_1x_0+a_2) - 6a_3 & = & 0 \\\end{array}\end{array}\right. .$

Ce système étant non linéaire, nous procéderons à sa résolution approchée à l’aide de la méthode de Newton. Pour cela, la matrice jacobienne correspondante sera nécessaire.

Matrice jacobienne

Dans ce qui suit, on note : $P_0(x) = a_0x^2+a_1x+a_2$ .

Voici les $7$ premières colonnes de la matrice jacobienne, elles contiennent les dérivées partielles selon les paramètres $a_0$ à $a_6$ :

$\left(\begin{array}{*3{>{\displaystyle}c}|*4{>{\displaystyle}c}|*1{>{\displaystyle}c}}E_1 & E_2 & E_3 & 0 & 0 & 0 & 0 & \multirow{4}{*}{\text{$(\ast)$}} \\\multicolumn{3}{c|}{\multirow{3}{*}{\text{$(0)$}}} & x_0^3 & x_0^2 & x_0 & 1 \\\multicolumn{3}{c|}{} & x_1^3 & x_1^2 & x_1 & 1 \\\multicolumn{3}{c|}{} & \multicolumn{4}{c|}{\text{$(0)$}} \\\hline & & & & & & & \\E_4 & E_5 & E_6 & -3x_0^2 & -2x_0 & -1 & 0 & \multirow{3}{*}{\text{$(\ast)$}} \\\multicolumn{3}{c|}{\multirow{2}{*}{\text{$(0)$}}} & 3x_1^2 & 2x_1 & 1 & 0 \\\multicolumn{3}{c|}{} & \multicolumn{4}{c|}{\text{$(0)$}} \\\hline & & & & & & & \\E_7 & E_8 & E_9 & -6x_0 & -2 & 0 & 0 & \multirow{3}{*}{\text{$(\ast)$}} \\\multicolumn{3}{c|}{\multirow{2}{*}{\text{$(0)$}}} & 6x_1 & 2 & 0 & 0 \\\multicolumn{3}{c|}{} & \multicolumn{4}{c|}{\text{$(0)$}} \\\hline & & & & & & & \\E_{10} & E_{11} & E_{12} & -6 & 0 & 0 & 0 & \text{$(\ast)$} \\\end{array}\right).$

Avec :

$E_1 = x_0^2 \exp(P_0(x_0)) ,$

$E_2 = x_0 \exp(P_0(x_0)) ,$

$E_3 = \exp(P_0(x_0)) ,$

$E_4 = x_0 (2 a_0 x_0^2 + a_1 x_0 + 2) \exp(P_0(x_0)) ,$

$E_5 = (2 a_0 x_0^2 + a_1 x_0 + 1) \exp(P_0(x_0)) ,$

$E_6 = (2 a_0 x_0 + a_1 ) \exp(P_0(x_0)) ,$

$E_7 = (4 a_0^2 x_0^4 + 2 a_0 x_0^2 (2 a_1 x_0 + 5) + a_1^2 x_0^2 + 4 a_1 x_0 + 2) \exp(P_0(x_0)) ,$

$E_8 = (4 a_0^2 x_0^3 + 2 a_0 x_0 (2 a_1 x_0 + 3) + a_1 (a_1 x_0 + 2)) \exp(P_0(x_0)) ,$

$E_9 = (4 a_0 x_0 (a_0 x_0 + a_1) + 2 a_0 + a_1^2) \exp(P_0(x_0)) ,$

$E_{10} = (8 a_0^3 x_0^5 + 12 a_0^2 x_0^3 (a_1 x_0 + 3) + 6 a_0 x_0 (a_1^2 x_0^2 + 5 a_1 x_0 + 4) + a_1 (a_1^2 x_0^2 + 6 a_1 x_0 + 6)) \exp(P_0(x_0)) ,$

$E_{11} = (8 a_0^3 x_0^4 + 12 a_0^2 a_1 x_0^3 + 24 a_0^2 x_0^2 + 6 a_0 a_1^2 x_0^2 + 18 a_0 a_1 x_0 + 6 a_0 + a_1^3 x_0 + 3 a_1^2) \exp(P_0(x_0)) ,$

$E_{12} = (2 a_0 x_0 + a_1) (4 a_0^2 x_0^2 + 4 a_0 a_1 x_0 + 6 a_0 + a_1^2) \exp(P_0(x_0)).$

Pour tout $k\in\llbracket 2 ; n-2 \rrbracket$ , voici les colonnes ${4k-5}$ à ${4k+6}$ de la matrice jacobienne, elles contiennent les dérivées partielles selon les paramètres $a_{4k-5}$ à $a_{4k+6}$ :

$\left(\begin{array}{*1{>{\displaystyle}c}|*4{>{\displaystyle}c}|*4{>{\displaystyle}c}|*4{>{\displaystyle}c}|*1{>{\displaystyle}c}}\multirow{9}{*}{\text{$(\ast)$}} & \multicolumn{4}{c|}{\text{$(0)$}} & \multicolumn{4}{c|}{\multirow{3}{*}{\text{$(0)$}}} & \multicolumn{4}{c|}{\multirow{5}{*}{\text{$(0)$}}} & \multirow{9}{*}{\text{$(\ast)$}} \\& x_{k-2}^3 & x_{k-2}^2 & x_{k-2} & 1 & \multicolumn{4}{c|}{} & \multicolumn{4}{c|}{} & \\& x_{k-1}^3 & x_{k-1}^2 & x_{k-1} & 1 & \multicolumn{4}{c|}{} & \multicolumn{4}{c|}{} & \\& \multicolumn{4}{c|}{\multirow{5}{*}{\text{$(0)$}}} & x_{k-1}^3 & x_{k-1}^2 & x_{k-1} & 1 & \multicolumn{4}{c|}{} & \\& \multicolumn{4}{c|}{} & x_{k}^3 & x_{k}^2 & x_{k} & 1 & \multicolumn{4}{c|}{} & \\& \multicolumn{4}{c|}{} & \multicolumn{4}{c|}{\multirow{2}{*}{\text{$(0)$}}} & x_{k}^3 & x_{k}^2 & x_{k} & 1 & \\& \multicolumn{4}{c|}{} & \multicolumn{4}{c|}{} & x_{k+1}^3 & x_{k+1}^2 & x_{k+1} & 1 & \\& \multicolumn{4}{c|}{} & \multicolumn{4}{c|}{} & \multicolumn{4}{c|}{\text{$(0)$}} & \\\hline & & & & & & & & & & & & & \\\multirow{6}{*}{\text{$(\ast)$}} & \multicolumn{4}{c|}{\text{$(0)$}} & \multicolumn{4}{c|}{\multirow{2}{*}{\text{$(0)$}}} & \multicolumn{4}{c|}{\multirow{3}{*}{\text{$(0)$}}} & \multirow{6}{*}{\text{$(\ast)$}} \\& -3x_{k-2}^2 & -2x_{k-2} & -1 & 0 & \multicolumn{4}{c|}{} & \multicolumn{4}{c|}{} & \\& 3x_{k-1}^2 & 2x_{k-1} & 1 & 0 & -3x_{k-1}^2 & -2x_{k-1} & -1 & 0 & \multicolumn{4}{c|}{} & \\& \multicolumn{4}{c|}{\multirow{3}{*}{\text{$(0)$}}} & 3x_{k}^2 & 2x_{k} & 1 & 0 & -3x_{k}^2 & -2x_{k} & -1 & 0 & \\& \multicolumn{4}{c|}{} & \multicolumn{4}{c|}{\multirow{2}{*}{\text{$(0)$}}} & 3x_{k+1}^2 & 2x_{k+1} & 1 & 0 & \\& \multicolumn{4}{c|}{} & \multicolumn{4}{c|}{} & \multicolumn{4}{c|}{\text{$(0)$}} & \\\hline\multirow{6}{*}{\text{$(\ast)$}} & \multicolumn{4}{c|}{\text{$(0)$}} & \multicolumn{4}{c|}{\multirow{2}{*}{\text{$(0)$}}} & \multicolumn{4}{c|}{\multirow{3}{*}{\text{$(0)$}}} & \multirow{6}{*}{\text{$(\ast)$}} \\& -6x_{k-2} & -2 & 0 & 0 & \multicolumn{4}{c|}{} & \multicolumn{4}{c|}{} & \\& 6x_{k-1} & 2 & 0 & 0 & -6x_{k-1} & -2 & 0 & 0 & \multicolumn{4}{c|}{} & \\& \multicolumn{4}{c|}{\multirow{3}{*}{\text{$(0)$}}} & 6x_{k} & 2 & 0 & 0 & -6x_{k} & -2 & 0 & 0 & \\& \multicolumn{4}{c|}{} & \multicolumn{4}{c|}{\multirow{2}{*}{\text{$(0)$}}} & 6x_{k+1} & 2 & 0 & 0 & \\& \multicolumn{4}{c|}{} & \multicolumn{4}{c|}{} & \multicolumn{4}{c|}{\text{$(0)$}} & \\\hline & & & & & & & & & & & & & \\{\text{$(\ast)$} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \text{$(\ast)$} \\\end{array}\right).$

Dans ce qui suit, on note $P_{4n-1}(x) = a_{4n-1}x+a_{4n}$ .

Voici les $6$ dernières colonnes de la matrice jacobienne, elles contiennent les dérivées partielles selon les paramètres $a_{4n-5}$ à $a_{4n}$ :

$\left(\begin{array}{*1{>{\displaystyle}c}|*4{>{\displaystyle}c}|*2{>{\displaystyle}c}}\multirow{4}{*}{\text{$(\ast)$}} & \multicolumn{4}{c|}{\text{$(0)$}} & \multicolumn{2}{c}{\multirow{3}{*}{\text{$(0)$}}} \\& x_{n-2}^3 & x_{n-2}^2 & x_{n-2} & 1 & \multicolumn{2}{c}{} \\& x_{n-1}^3 & x_{n-1}^2 & x_{n-1} & 1 & \multicolumn{2}{c}{} \\& 0 & 0 & 0 & 0 & E'_{1} & E'_{2} \\\hline & & & & & & \\\multirow{3}{*}{\text{$(\ast)$}} & \multicolumn{4}{c|}{\text{$(0)$}} & \multicolumn{2}{c}{\multirow{2}{*}{\text{$(0)$}}} \\& -3x_{n-2}^2 & -2x_{n-2} & -1 & 0 & \multicolumn{2}{c}{} \\& 3x_{n-1}^2 & 2x_{n-1} & 1 & 0 & E'_{3} & E'_{4} \\\hline & & & & & & \\\multirow{3}{*}{\text{$(\ast)$}} & \multicolumn{4}{c|}{\text{$(0)$}} & \multicolumn{2}{c}{\multirow{2}{*}{\text{$(0)$}}} \\& -6x_{n-2} & -2 & 0 & 0 & \multicolumn{2}{c}{} \\& 6x_{n-1} & 2 & 0 & 0 & E'_{5} & E'_{6} \\\hline & & & & & & \\\text{$(\ast)$} & 0 & 0 & 0 & 0 & 0 & 0 \\\end{array}\right).$

Avec :

$E'_1 = -x_{n-1} \exp(P_{4n-1}(x_{n-1})) ,$

$E'_2 = -\exp(P_{4n-1}(x_{n-1})) ,$

$E'_3 = (a_{4n-1} + 1)\exp(P_{4n-1}(x_{n-1})) ,$

$E'_4 = a_{4n-1} \exp(P_{4n-1}(x_{n-1})) ,$

$E'_5 =(a_{4n-1}^2x_{n-1} + 2a_{4n-1}) \exp(P_{4n-1}(x_{n-1})) ,$

$E'_6 = a_{4n-1}^2 \exp(P_{4n-1}(x_{n-1})).$

Résultats

Nous avons testé cette méthode en utilisant les données des salaires nets équivalent temps plein de 2020 (figure complémentaire 4 du fichier xls fourni par l’INSEE sur cette page). Pour cela, nous avons utilisé les 10ème, 25ème, 50ème, 75ème, 90ème et 95ème centiles (qui sont disponibles pour la plupart des années) pour servir de base à l’optimisation, et les autres centiles disponibles (du 5ème au 99ème) pour tester la justesse de notre fonction d’estimation.
La valeur initiale du vecteur de paramètres est déterminée de telle façon que les points servant de base à l’interpolation soient reliés par des segments de droite, et que les exponentielles des intervalles extrêmes soient raccordées de manière $\mathcal{C}^1$ au segment le plus proche.

On peut tout d’abord constater une convergence assez rapide. Seules 6 itérations de la méthode de Newton sont nécessaires pour que la norme de la différence entre deux valeurs successives du vecteur de paramètres $a$ devienne inférieure à $10^{-15}$ . Le processus de convergence est illustré par les figures 1 et 2.

Fig 1. Convergence de l’approximation de la fonction de répartition

Fig 2. Convergence de la fonction de densité correspondante (dérivée de la fonction de répartition)

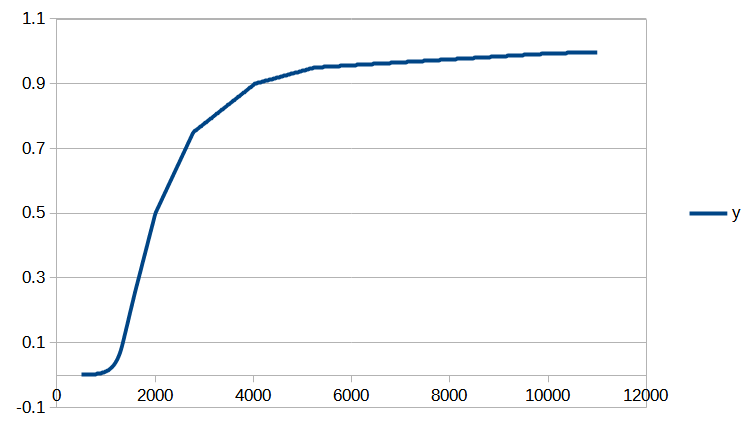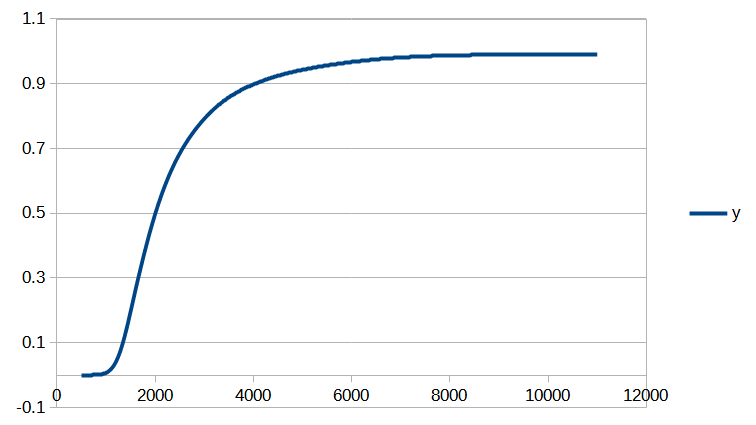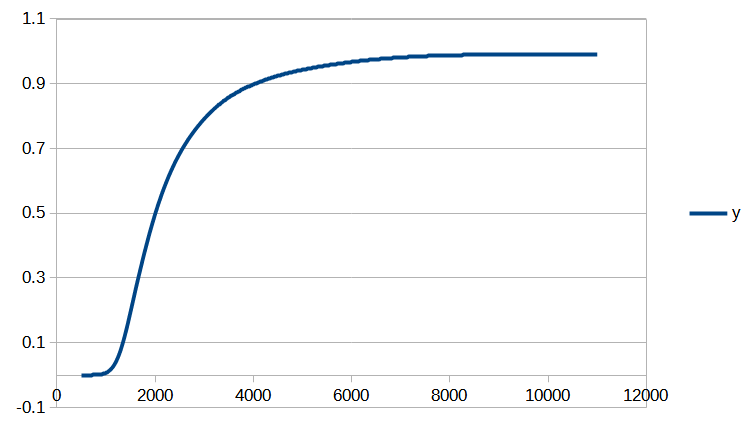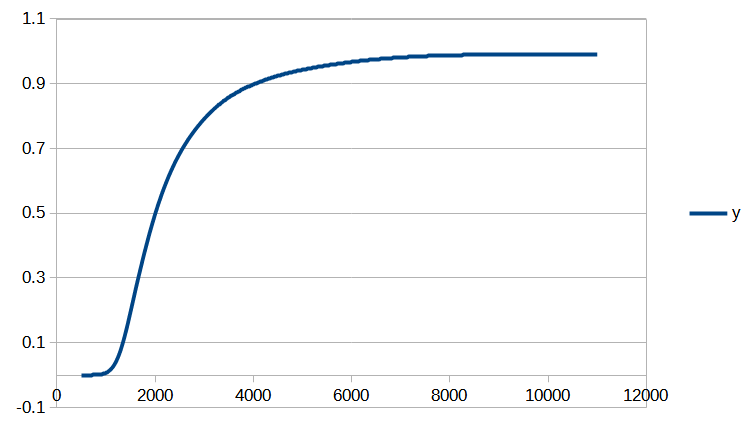
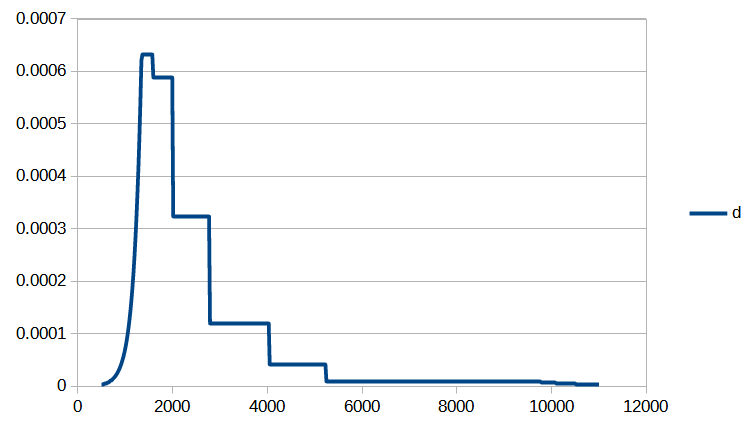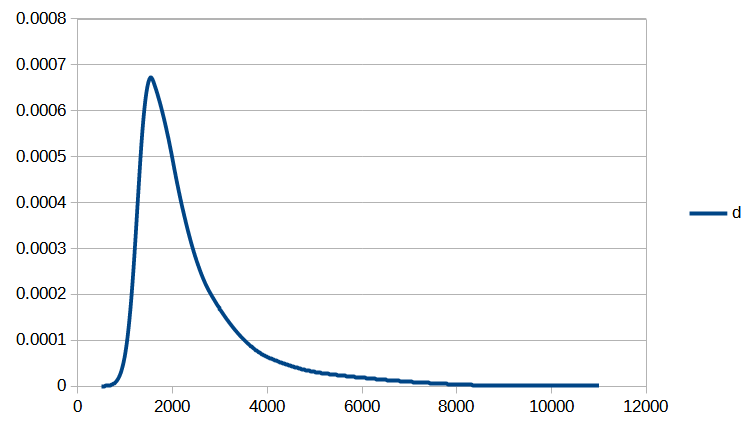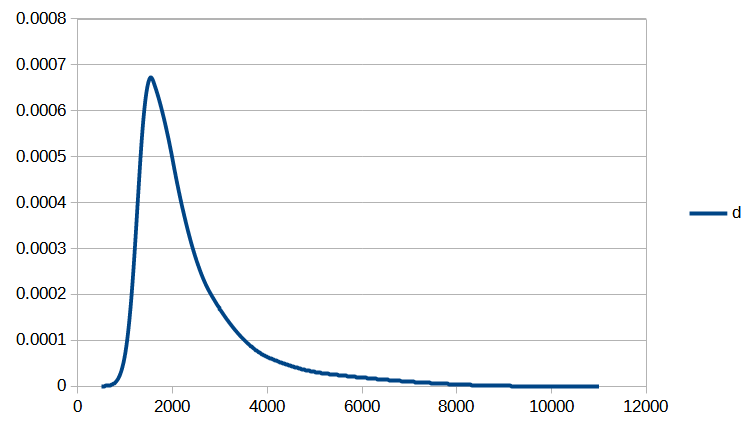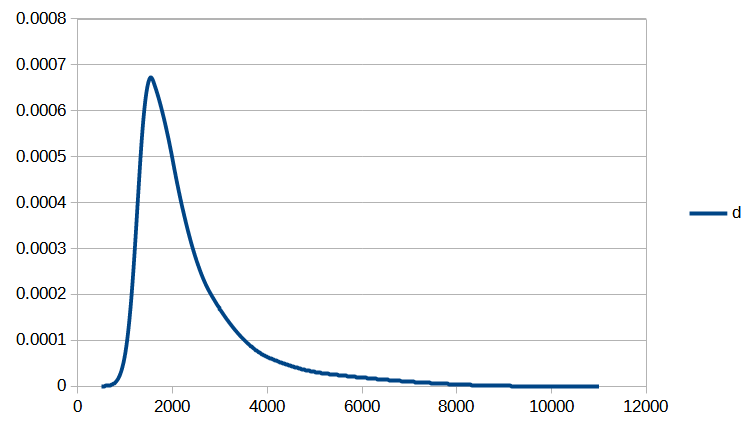
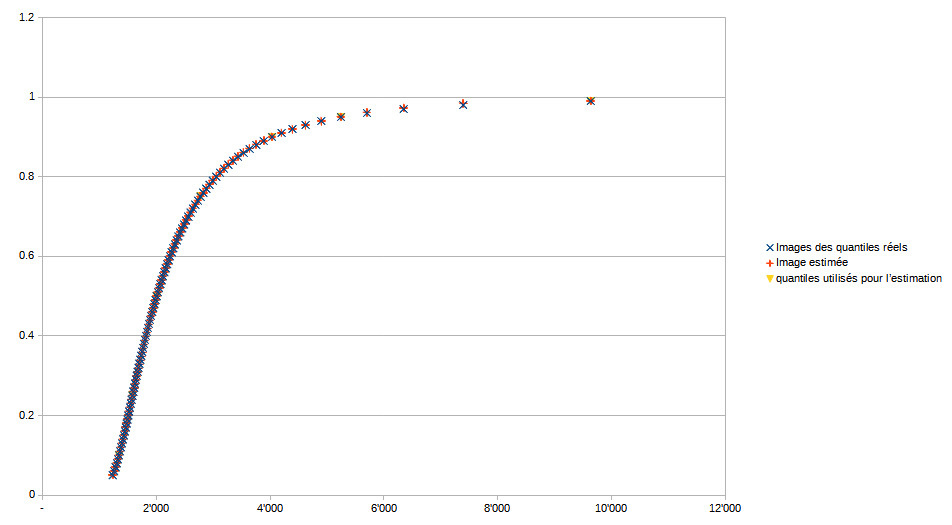
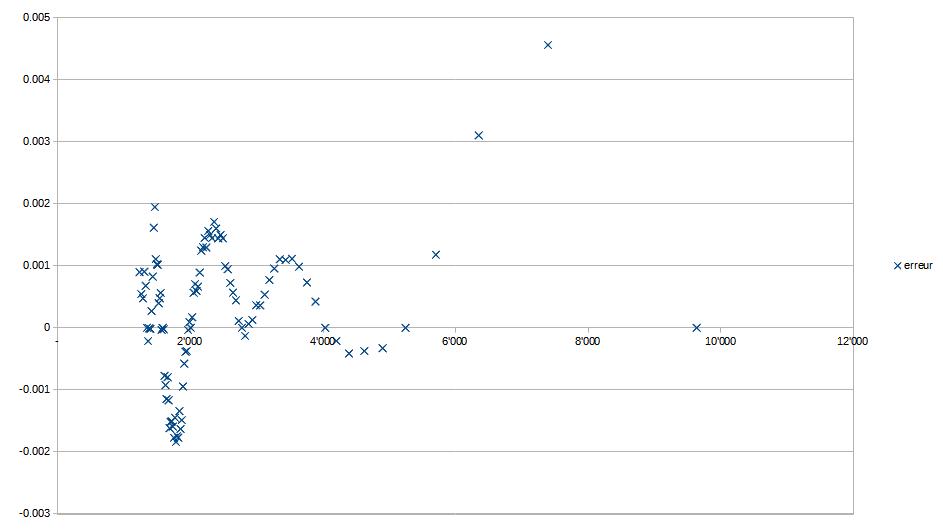
On peut maintenant comparer l’image de l’ensemble des centiles disponibles dans le tableau de l’INSEE aux valeurs calculées à l’aide de la fonction de répartition obtenue avec notre méthode (Fig 3.). On constate que l’erreur n’excède pas 0,2% jusqu’au 96ème centile inclus, et reste inférieure à 0,5% pour les centiles restants (Fig 4).

Introduction

Fonction utilisée pour approximer la fonction de répartition

Système d’équations à résoudre

Matrice jacobienne

Résultats

Laisser un commentaire Annuler la réponse