[ MAJ du 28/06/2023 : le modèle présenté dans cet article a été étoffé ici.]
Introduction
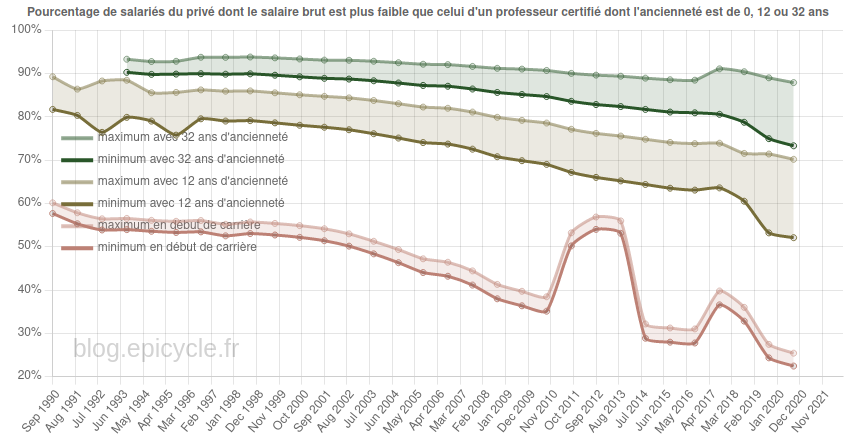
Cet article est assez technique et est destiné à documenter le calcul de la position d’un salaire dans la distribution des salaires du secteur privé dans notre Observatoire des salaires des enseignants.
Si vous êtes intéressé par les animations de convergence et la précision obtenue, rendez-vous directement dans la dernière partie de l’article, mais si vous avez quelques bases en analyse numérique et êtes intéressé par le type d’interpolation utilisé, vous pourrez trouver dans ce qui suit quelques indications sur la méthode que nous avons utilisée.