Dans son rapport sur l’évolution du métier d’enseignant, le cabinet McKinsey propose l’idée de rémunérer les enseignants au mérite, et utilise, en guise d’argument, une affirmation de l’OCDE selon laquelle la rémunération au mérite permet d’améliorer les résultats des élèves lorsque les professeurs sont mal payés (comme en France) tandis que cela aurait l’effet inverse lorsque les professeurs sont bien payés.
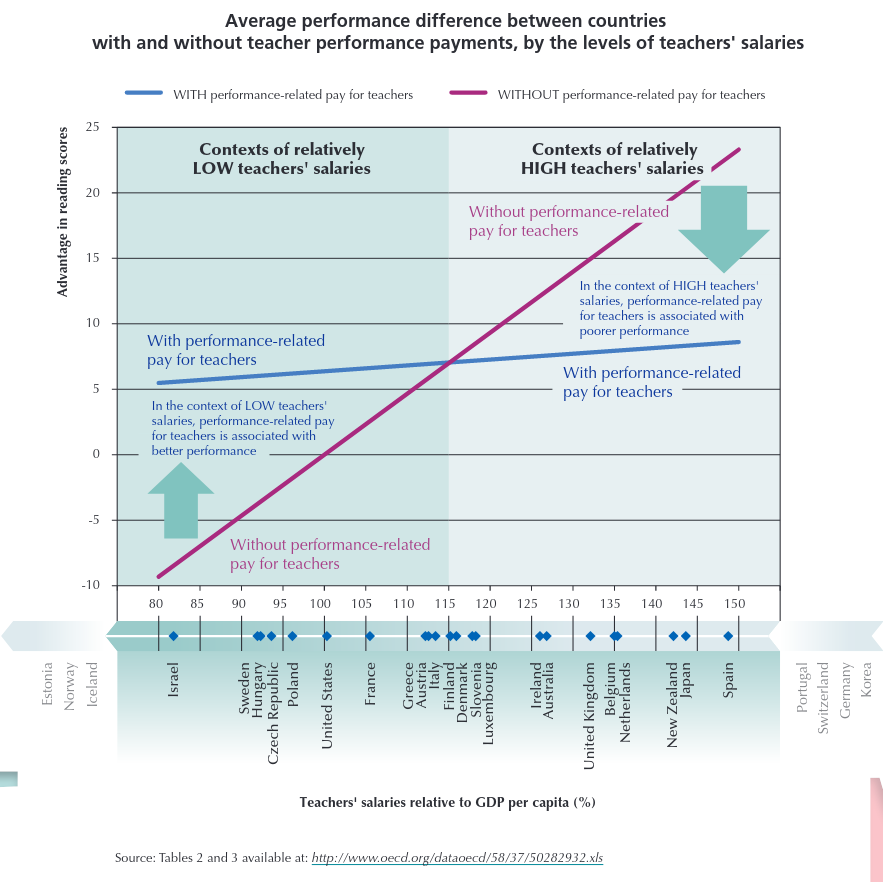
Cette affirmation se base le graphique suivant, issu d’un document de l’OCDE intitulé Does performance-based pay improve teaching ?
Ce graphique a été repris, moyennant quelques variations visuelles, dans la page 38 du document Approfondissement Valorisation du Mérite_vf de McKinsey, que vous trouverez en fin d’article :
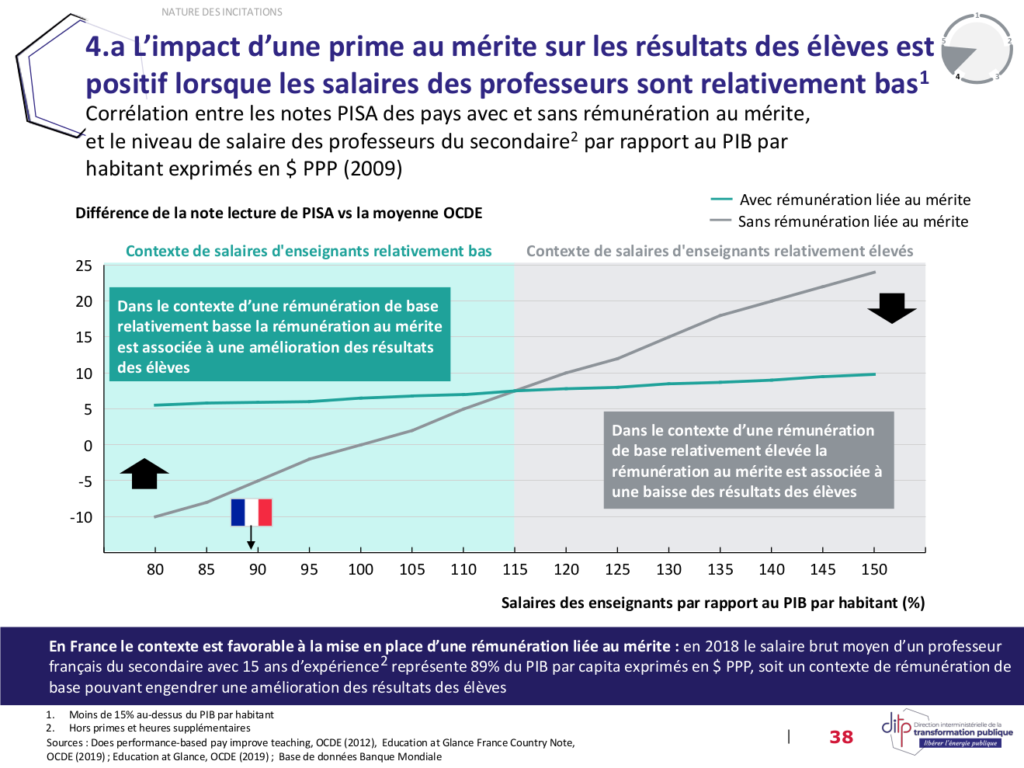
Ce modèle suggère également que les résultats des élèves sont positivement corrélés à la rémunération de base des enseignants. Cette proposition n’est cependant pas évoquée.
Nous pouvons afficher les nuages de points issus des données brutes fournies avec l’étude ainsi que leurs droites de régression linéaire respectives. Je vous laisse juge de la pertinence de résumer ces données par une simple droite :
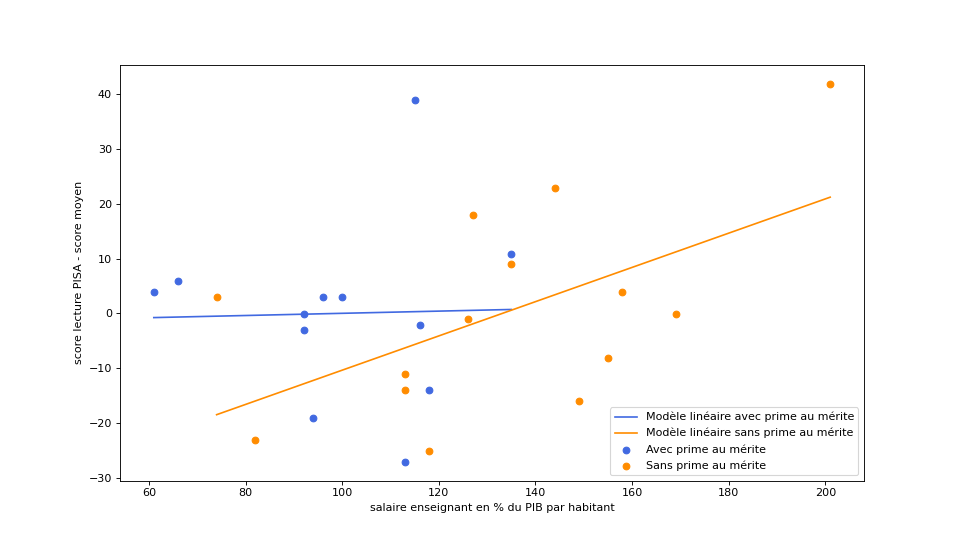
Les points pouvant s’éloigner très fortement des droites qui sont censées les modéliser, il semble peu judicieux d’utiliser celles-ci avec une visée prédictive.
Pour juger de la pertinence de ce modèle, il est également intéressant de jeter un œil à deux grandeurs annexes :
- L’intervalle de confiance, qui permet de visualiser l’incertitude sur l’emplacement de la droite, est une zone dans laquelle la droite a, compte-tenu de la variabilité des données, 95% de chances de se trouver.
- L’intervalle de fluctuation, qui permet de visualiser l’incertitude sur l’emplacement des données, est une zone dans laquelle celles-ci ont 95% de chances de se trouver.
On obtient alors le graphique suivant :
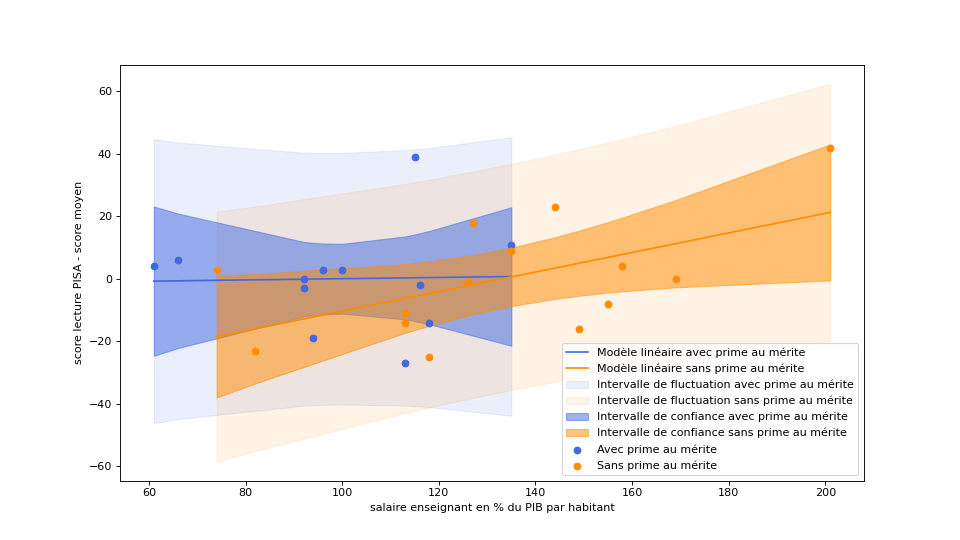
On peut constater sur celui-ci qu’il y a une forte incertitude sur le modèle, l’intervalle de confiance de chacune des droites nous indiquant qu’il y a une probabilité non négligeable pour que la droite bleue des pays qui pratiquent la prime au mérite soit en réalité en-dessous de la droite orange des pays qui ne la pratiquent pas.
De plus, les intervalles de fluctuation se recouvrent de manière tellement large qu’il est impossible d’affirmer qu’un pays qui mettrait en place une prime au mérite (ou l’abandonnerait) puisse constater un effet sur les performances des élèves.
On notera également qu’aucune donnée des pays pratiquant la prime au mérite ne se trouve dans la partie droite du graphique, ce qui n’a pas empêché l’OCDE de prolonger la droite correspondante afin d’en conclure quelque chose pour les pays dans lesquels les professeurs sont bien payés. On remarquera cependant que les pays dans lesquels les professeurs sont bien rémunérés ne pratiquent pas la prime au mérite.
Le document technique fourni par l’OCDE nous indique que leur analyse est en réalité plus complexe qu’une simple régression linéaire et inclut des données qui ne sont pas présentes dans le fichier xls fourni avec l’étude, ainsi que des variables qui sont passées sous silence dans le document principal.
Si d’autres variables permettent d’expliquer les fortes variations observées lorsqu’on compare la performance des élèves en lecture et le salaire des enseignants ramené au PIB par habitant, ces variables devraient être mentionnées dans le document principal. Cela signifie qu’il existe d’autres leviers dont il serait intéressant de quantifier les effets.
Par ailleurs, si la corrélation est significative, cela implique que les données se trouvent proches d’un hyperplan qui ne saurait être résumé par une unique droite :
– d’une part, rien ne nous garantit que les deux droites soient dans la même position l’une par rapport à l’autre si on observe une autre intersection des hyperplans correspondants ;
– d’autre part, l’incertitude due à la variabilité des données devrait être quantifiée en faisant apparaître les intervalles de confiance et de fluctuation des hyperplans : plus cette dispersion est importante, plus la valeur prédictive du modèle est faible.
On peut également lire dans ce document technique que le Canada, le Chili, la France, le Mexique, la Nouvelle-Zélande, la Slovaquie et la Turquie ont été exclues de l’étude en raison de données manquantes. On constate cependant que pour 4 de ces pays, la pratique de la prime au mérite est connue, et que chacun de ces pays a un score de lecture inférieur à la moyenne des pays retenus pour l’étude (qui est de 497). Ce score de lecture est même inférieur pour 3 d’entre eux à celui de l’Autriche (qui est de 470, score le plus faible de toute l’étude).
| Pays | Performance moyenne en lecture | Prime au mérite | Salaire des enseignants en % du PIB/hab. |
|---|---|---|---|
| Canada | 524 | n.c. | n.c. |
| Chili | 449 | oui | n.c |
| France | 496 | n.c. | 105 |
| Mexique | 425 | oui | n.c |
| Nouvelle-Zélande | 521 | n.c. | 142 |
| Slovaquie | 477 | oui | n.c. |
| Turquie | 464 | oui | n.c. |
Ajouter ces 4 pays ayant de faibles performances en lecture aux 12 points de données existants est susceptible de déplacer la droite bleue (plus exactement l’hyperplan sous-jacent) vers le bas du graphique, et possiblement modifier sa pente, ce qui peut radicalement changer les conclusions de l’étude.
Un grand merci à @JulienGossa et @_MickaelM_ pour avoir initié la réflexion.
Code Python utilisé pour générer les graphiques :
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
import statsmodels.formula.api as smf
df = pd.read_csv('perf_remu_OCDE.csv')
moyenne = df['Mean_perf'].mean();
df['Mean_perf']-=moyenne
df['YSALARY']*=100
df.sort_values(by=['YSALARY'], inplace=True)
df_oui = df.loc[df['TPP']=='oui']
df_non = df.loc[df['TPP']=='non']
name_x = 'salaire enseignant en % du PIB par habitant'
name_y = 'score lecture PISA - score moyen'
name_hue = 'prime au mérite'
alpha = .05
results1 = smf.ols('Mean_perf ~ YSALARY', df_oui).fit()
predictions1 = results1.get_prediction(df_oui).summary_frame(alpha)
results2 = smf.ols('Mean_perf ~ YSALARY', df_non).fit()
predictions2 = results2.get_prediction(df_non).summary_frame(alpha)
x1 = df_oui['YSALARY']
y1 = df_oui['Mean_perf']
x2 = df_non['YSALARY']
y2 = df_non['Mean_perf']
fig, ax = plt.subplots(figsize=(12, 6.75), dpi=80)
ax.fill_between(x1, predictions1['obs_ci_lower'], predictions1['obs_ci_upper'], alpha=.1, color='royalblue', label='Intervalle de fluctuation avec prime au mérite')
ax.fill_between(x2, predictions2['obs_ci_lower'], predictions2['obs_ci_upper'], alpha=.1, color='darkorange', label='Intervalle de fluctuation sans prime au mérite')
ax.fill_between(x1, predictions1['mean_ci_lower'], predictions1['mean_ci_upper'], alpha=.5, color='royalblue', label='Intervalle de confiance avec prime au mérite')
ax.fill_between(x2, predictions2['mean_ci_lower'], predictions2['mean_ci_upper'], alpha=.5, color='darkorange', label='Intervalle de confiance sans prime au mérite')
ax.plot(x1, predictions1['mean'], color='royalblue', label='Modèle linéaire avec prime au mérite')
ax.plot(x2, predictions2['mean'], color='darkorange', label='Modèle linéaire sans prime au mérite')
ax.scatter(x1, y1, label='Avec prime au mérite', marker='o', color='royalblue')
ax.scatter(x2, y2, label='Sans prime au mérite', marker='o', color='darkorange')
plt.xlabel(name_x)
plt.ylabel(name_y)
plt.legend(loc ="lower right")
fig.savefig('data.png')Fichier csv contenant les données utilisées par le programme :
Annexes d’approfondissement du rapport McKinsey :