À l’occasion de la sortie de son rapport Regards sur l’éducation 2023, l’OCDE a publié les données concernant le pouvoir d’achat des enseignants en 2022.
Ceci nous permet donc de faire le bilan du ministère de Jean-Michel Blanquer, qui promettait sur France Inter le 26 février 2020 de « faire du professeur français un des professeurs les mieux payés d’Europe […] en mettant le paquet », celui-ci ayant quitté ses fonctions de ministre de l’Éducation nationale, de la Jeunesse et des Sports le 20 mai 2022.
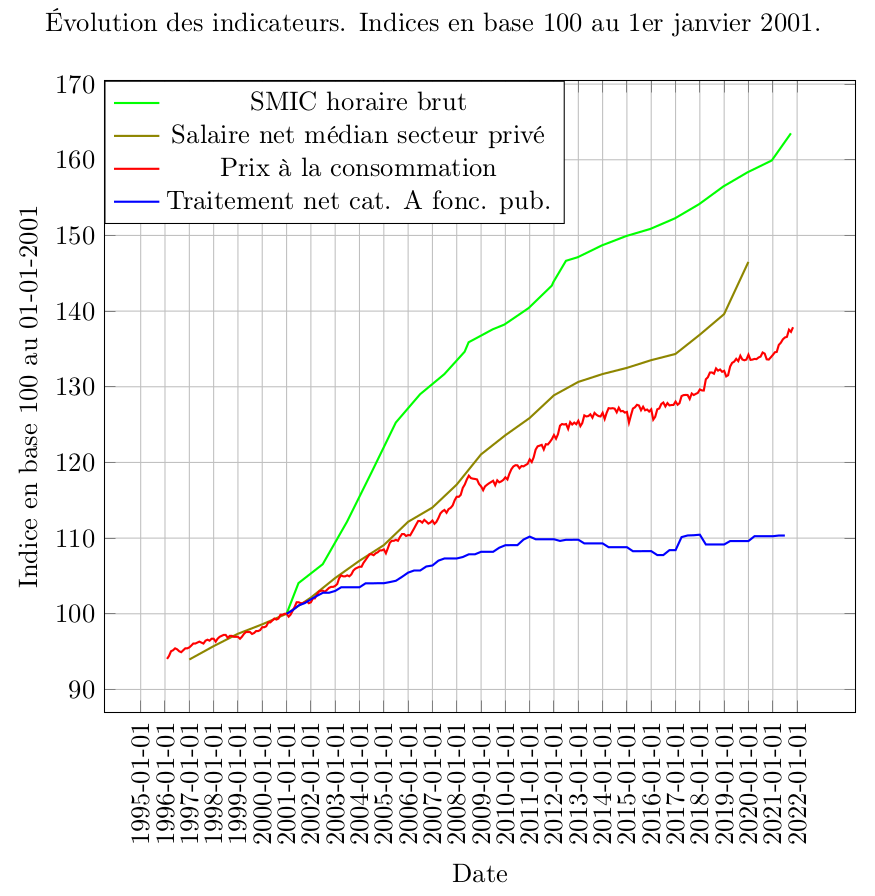
Évolution du pouvoir d’achat des enseignants de 1990 à 2023, un point d’étape
Les salaires statutaires des enseignants de l’Éducation nationale ont bénéficié ces dernières années de quelques augmentations ciblant essentiellement les débuts de carrière. Au moment de l’écriture de cet article, la dernière de ces hausses a eu lieu en septembre 2023. Celle-ci n’a été que de 5,5% en moyenne, alors que la promesse de campagne d’Emmanuel Macron était une augmentation inconditionnelle de 10% pour l’ensemble des enseignants.
Suite à la publication des chiffres de l’inflation de septembre 2023 par l’INSEE, notre Observatoire des salaires des enseignants permet désormais d’évaluer l’évolution du pouvoir d’achat des enseignants entre septembre 1990 et septembre 2023. Les tableaux suivants indiquent les évolutions constatées sur cette période à différents stades d’ancienneté. On y constate une baisse de pouvoir d’achat dans l’écrasante majorité des cas.
Heures supplémentaires pour les enseignants du second degré : entre flexibilité, maîtrise des coûts, et augmentation du temps de travail
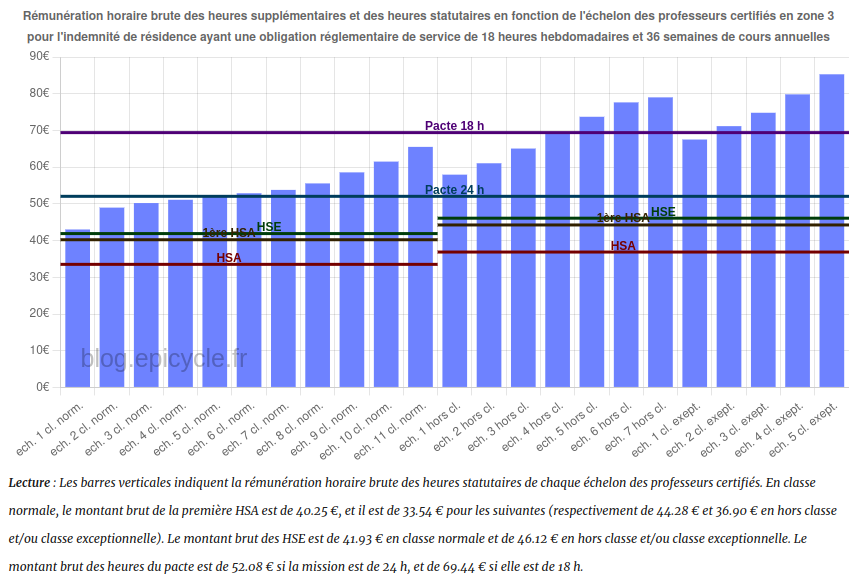
Depuis près de 20 ans, les enseignants du second degré effectuent de plus en plus d’heures supplémentaires alors même que celles-ci sont moins bien rémunérées que les heures relevant de leur service normal.
En contradiction avec les remontées des chefs d’établissements, qui insistent sur la nécessité du volontariat, une deuxième heure supplémentaire peut être imposée aux enseignants depuis 2019 (décret n°2019-309 du 11 avril 2019), et la Cour des comptes va même jusqu’à recommander en 2020 d’inclure ces deux heures supplémentaires non refusables dans le temps de service statutaire des enseignants.
Le Pacte consiste depuis septembre 2023 en de nouvelles tâches supplémentaires proposées aux enseignants (décret n°2023-627 du 19 juillet 2023). Celles-ci sont en général mieux rémunérées que les autres heures supplémentaires mais ne peuvent pas être effectuées en lieu et place des heures supplémentaires non refusables, ce qui devrait aboutir à une nouvelle augmentation du temps de travail.
Continuer la lecture de « Heures supplémentaires pour les enseignants du second degré : entre flexibilité, maîtrise des coûts, et augmentation du temps de travail »Interpoler une fonction de répartition à partir de quantiles connus
Cet article poursuit le travail commencé ici en procédant à une généralisation du modèle utilisé.
Introduction
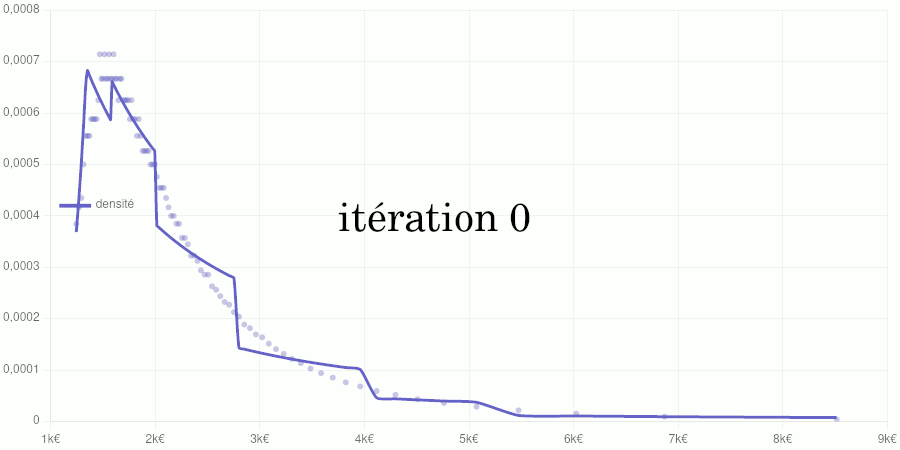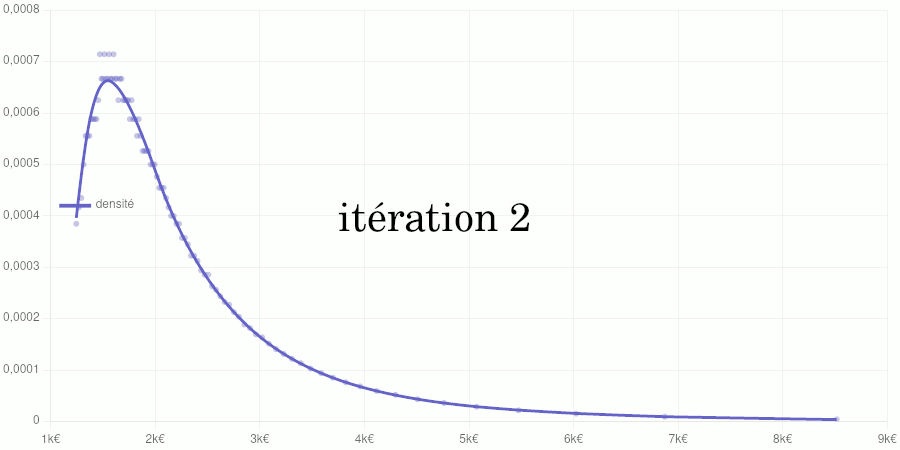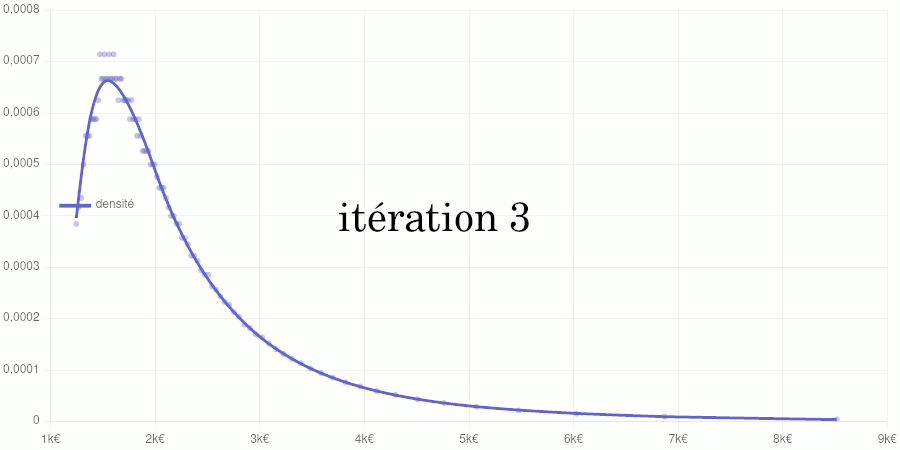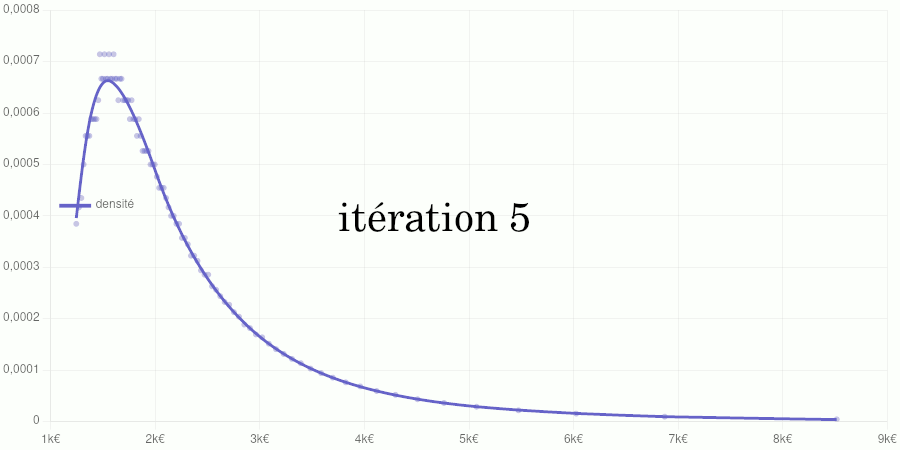
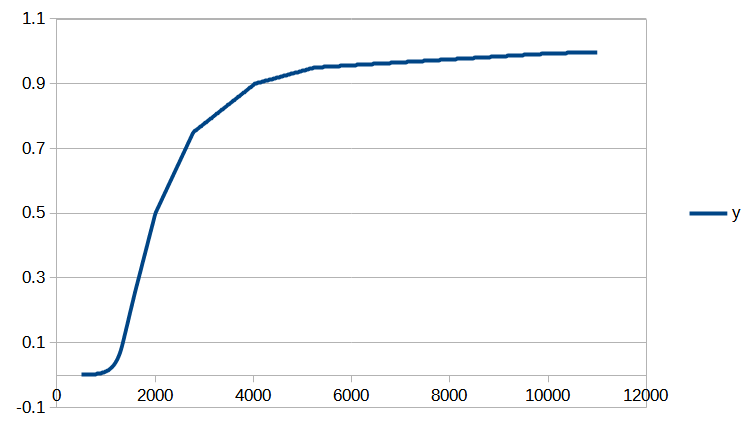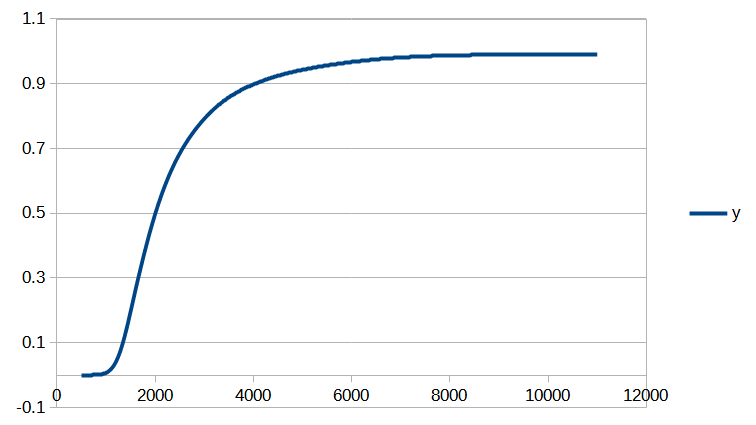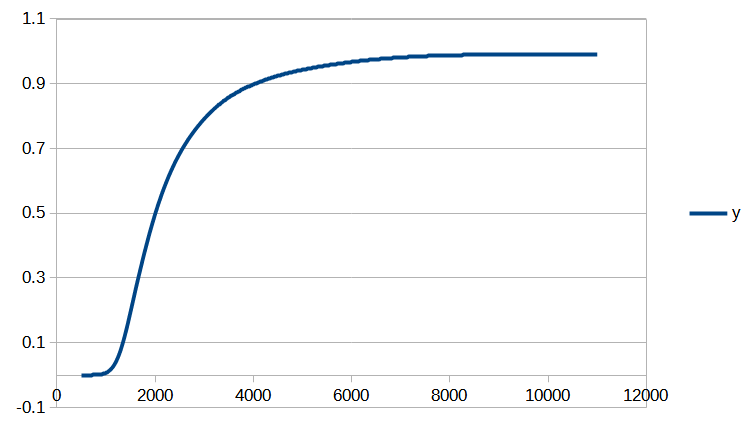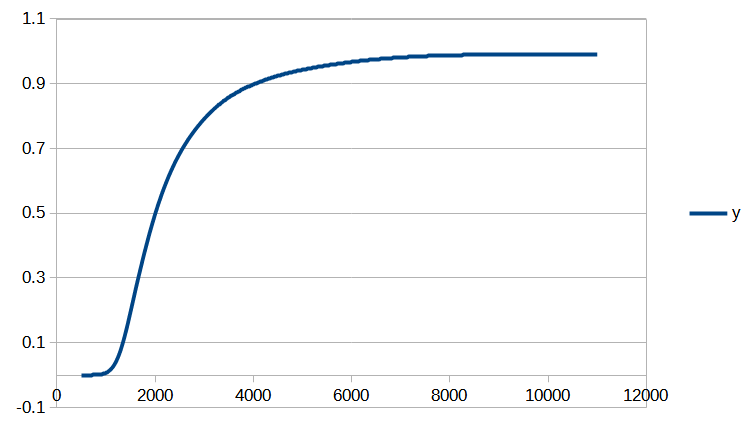
Cet article est assez technique et est destiné à documenter le calcul de la position d’un salaire dans la distribution des salaires du secteur privé dans notre Observatoire des salaires des enseignants ainsi que sur notre page Où vous trouvez-vous sur l’échelle des salaires ?.
Si vous êtes intéressé par les animations de convergence et la précision obtenue, rendez-vous directement dans la dernière partie de l’article, mais si vous avez quelques bases en analyse numérique et êtes intéressé par le type d’interpolation utilisé, vous pourrez trouver dans ce qui suit quelques indications sur la méthode que nous avons utilisée.
Quand McKinsey et l’OCDE oublient les données brutes et extrapolent sur la base d’un modèle peu convaincant
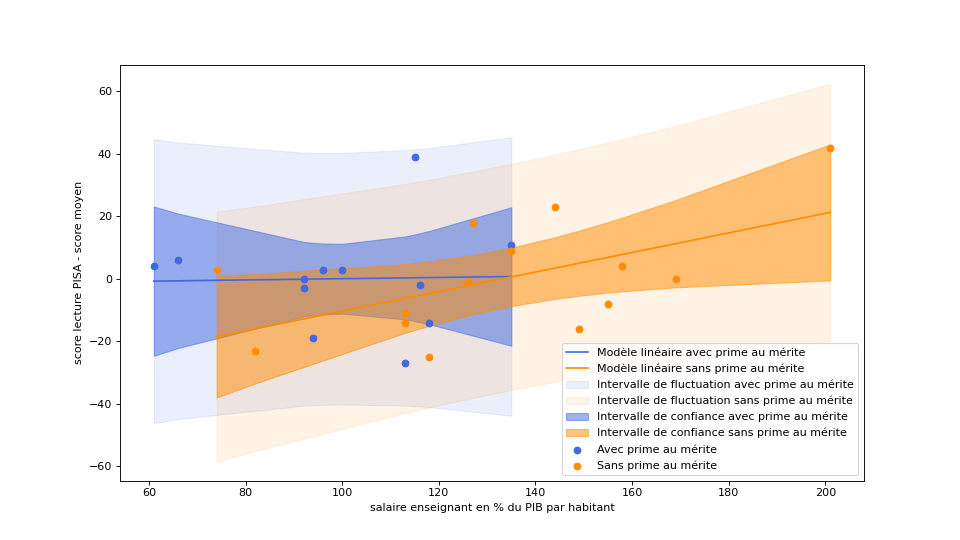
Dans son rapport sur l’évolution du métier d’enseignant, le cabinet McKinsey propose l’idée de rémunérer les enseignants au mérite, et utilise, en guise d’argument, une affirmation de l’OCDE selon laquelle la rémunération au mérite permet d’améliorer les résultats des élèves lorsque les professeurs sont mal payés (comme en France) tandis que cela aurait l’effet inverse lorsque les professeurs sont bien payés.
Continuer la lecture de « Quand McKinsey et l’OCDE oublient les données brutes et extrapolent sur la base d’un modèle peu convaincant »Interpoler une fonction de répartition des salaires à partir de quantiles connus
[ MAJ du 28/06/2023 : le modèle présenté dans cet article a été étoffé ici.]
Introduction
Cet article est assez technique et est destiné à documenter le calcul de la position d’un salaire dans la distribution des salaires du secteur privé dans notre Observatoire des salaires des enseignants.
Si vous êtes intéressé par les animations de convergence et la précision obtenue, rendez-vous directement dans la dernière partie de l’article, mais si vous avez quelques bases en analyse numérique et êtes intéressé par le type d’interpolation utilisé, vous pourrez trouver dans ce qui suit quelques indications sur la méthode que nous avons utilisée.
Salaires des professeurs de l’Éducation nationale : annonces grandiloquentes et déclassement au long cours
Depuis quelques années, les rares augmentations du salaire des enseignants font l’objet d’une communication qui n’est malheureusement pas en adéquation avec la réalité :
Continuer la lecture de « Salaires des professeurs de l’Éducation nationale : annonces grandiloquentes et déclassement au long cours »Évolutions comparées des salaires des enseignants français et de l’OCDE
[Les données de cet article ne sont plus maintenues. Veuillez vous rendre ici pour des données à jour.]
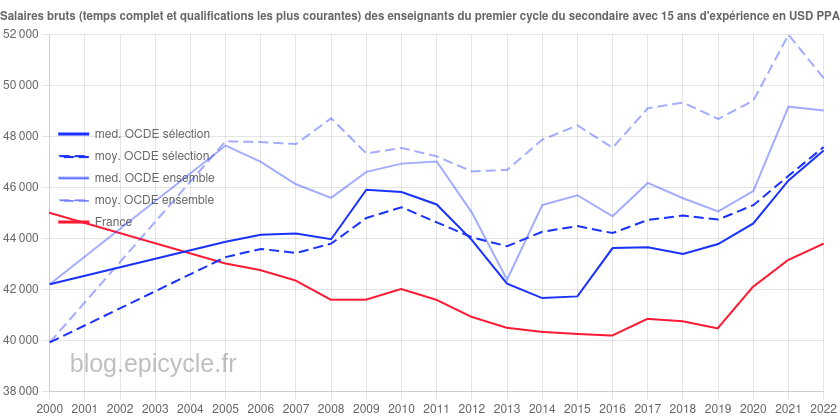
Afin d’approfondir la comparaison entres les salaires des enseignants de France et du reste de l’OCDE esquissée dans cet article, voici quatre graphiques concernant respectivement les enseignants :
– du deuxième cycle du secondaire ;
– du premier cycle du secondaire ;
– du primaire ;
– de l’éducation de la petite enfance.
Graphiques interactifs : évolution des salaires dans l’Éducation nationale
La page suivante vous propose quatre outils interactifs permettant de suivre le pouvoir d’achat des enseignants ainsi que leur place par rapport à la distribution des salaires dans le secteur privé.
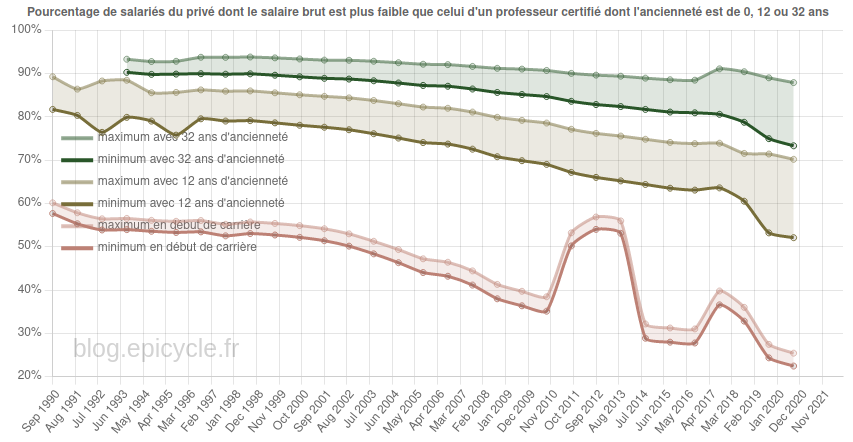
Déclassement des salaires : pourquoi il serait raisonnable d’augmenter les enseignants d’au moins 20% sans contrepartie
[MAJ du 16/12/2021]
La pétition dont il est question à la fin de cet article a été classée de manière prématurée hier par le président de la commission éducation de l’Assemblée Nationale : https://twitter.com/stylos_les/status/1471363208678154245
Il n’est donc plus possible de la signer, alors que son expiration devait initialement intervenir en juin 2022.